You got nothing on the 17 square packing
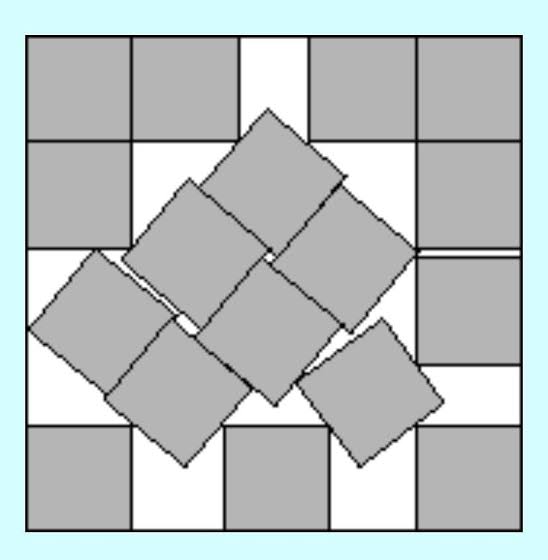
Can someone explain this?
We’ve figured out optimal packing methods for any number of squares inside a big square. When a number is below and near a square number like 15, you just leave an empty box, but when it’s far from the next square number, you’ll be able to pack them more efficiently than just leaving empty squares around. Turns out this kind of stuff is hilariously hard to prove that it’s the most efficient method.
This is the most efficient (known) packing of 17 unit squares inside a square. If you’re asking why it’s like that, that’s above my math proficiency level.
https://en.wikipedia.org/wiki/Square_packing
See also: https://kingbird.myphotos.cc/packing/squares_in_squares.html
It’s like that because the universe wants us to suffer.
If God was real / or is real and cared, we would have a perfect 336 day year.
No, suffering would be if it were always the same predictable pattern in everything all the time.
True. You can’t have joy without suffering, light without dark, cars without an extended warranty.
Thanks I’ve lost 30 sanity points now, and I’m now sure with a number of squares sufficently high s is gonna equal to cthulu.
?

This is about the most efficient way to pack that number of circles. By looking at the bottom row of the 49, you can see that it’s slightly less wide than 7 diameters, because it has 5 circles at the very bottom (taking up 5 diameters of width), but two are slightly raised, which also means they’re slightly inward.
Maths is a science now?
Science is applied math, engineering is applied science, manufacturing is applied engineering, etc. it’s math all the way down.

Math and philosophy are basically interchangeable here. I know there’s a maths version I saved somewhere. 😅
I mean without philosophy there is no math
And vice versa.
Wdym?
This is the kind of stuff the timber mafia needs to know so that they can efficiently pack trees and send them to IKEA.

Should have used hexagons
The bestagons.
I mean it makes sense when you think about how the circles arrange in an infinte square and e.g. 4r square. There has to be some fuckery between the perfect packing and the small square packing. You can see a triangle of almost perfect packing in the middle of the 49 circle square, surrounded by fault lines in the structure and then some more good packing, and garbage in the bottom.
slightly related Steve Mould video
Yarr
Neat spacing leave much gap, patterned mess less space between.
How?
Yes, if you push the circles down a bit, it forms a 7 by 7 matrix. But if pushing the circles into a square matrix is not allowed: how?
Edit: I get it now. It is about (efficient) packing not about counting. I also get the 4th panel now…
Yeah it can fit almost 7 in a line in the last panel so theese definitely aren’t the same squares(or circles)
These are optimal packings of n circles in a square container of the smallest size that will contain them
So it is fitting the 49 in smallest square and not fitting as many circles as possible in given square? Okay that makes sense
Correct!
7 by 7 matrix isn’t the optimal packing. The square shown is slightly smaller than 7 by 7.
Thanks. I thought it was about counting. It all makes a lot more sense now. (And it also doesn’t.)











